Tras la descripción en este blog de algunas de las técnicas metaheurísticas más clásicas como Colonia de Hormigas y su aplicación directa al cálculo de rutas, creo que es interesante analizar la forma en que algunas de las nuevas técnicas metaheurísticas, que no han nacido para dar solución a dicho problema, pueden gracias a las nuevas (o no tan nuevas) tecnologías, aplicarse para la resolución de este problema.
En esta entrada me gustaría presentar la Colonia de Abejas, una técnica introducida por D.Karaboga [1] en 2007 y que se basa en el proceso de búsqueda de néctar en las flores por parte de las abejas melíferas.
Modelo biológico
El modelo biológico básico de recolección de alimento de las abejas melíferas consta de los siguientes elementos:
- Fuentes de alimento: Puntos de extracción de alimento por parte de las abejas. Las fuentes de alimento tienen muchos factores como pueden ser la distancia con la colmena, la concentración de néctar, la dificultad de extracción, etc. Para nosotros, una fuente de alimento será una solución a nuestro problema, es decir, una ruta factible.
- Abejas recolectoras empleadas: Abejas asociadas a una fuente de alimento. Estas abejas comparten información sobre su fuente de alimento, como la ubicación o la concentración de néctar.
- Abejas recolectoras desempleadas: Abejas que no están asociadas a ninguna fuente de alimento. Existen dos tipos, las abejas exploradoras que se encargan de buscar nuevas fuentes de alimento (nuevas soluciones) y las abejas observadoras que esperan en la colmena a que una abeja empleada les de información sobre su fuente de alimento.
La forma de compartir información de las abejas recolectoras empleadas es por medio de una danza, cuya duración indica la concentración de néctar de la fuente de alimento, el ángulo con respecto al sol la dirección de la fuente y el número de movimientos zig-zag durante la danza representa la distancia. Cuanto más rentable resulte la fuente, más larga será la danza y por lo tanto, mayor será la probabilidad de que una abeja desempleada la observe y elija explotar dicha fuente de alimento.

Cuando se agotan las fuentes de alimento, las abejas empleadas en ellas se convierten en abejas desempleadas y tendrán que elegir entre esperar a recibir información de una abeja empleada sobre su fuente de alimento para explotarla o bien salir a buscar nuevas fuentes de alimento.
El algoritmo de colonia de abejas
El algoritmo de colonia de abejas intenta representar el comportamiento de éstas para encontrar soluciones a problemas de optimización. En el caso introducido por D.Karaboga, el cual voy a comenzar presentando, el lector va a comprobar que este algoritmo está pensado para problemas de optimización (lineal o no lineal), con variables continuas y para los que resulte sencillo obtener soluciones iniciales.
Una de las principales ventajas del algoritmo es que requiere un bajo número de parámetros:
- Número de soluciones (sol): El número de fuentes de alimento (soluciones iniciales factibles) para nuestro problema.
- Número de ciclos (n_iter): Número de iteraciones del algoritmo (también puede definirse un tiempo de ejecución).
- Límite (n_ciclos): Número de ciclos que se explota una fuente de alimento (se mejora una solución) antes de ser abandonada.
El algoritmo es el siguiente:
- Se comienza obteniendo un número «sol» de soluciones iniciales y evaluándolas. Cada una de estas soluciones iniciales representa una fuente de alimento en el modelo biológico.
- El siguiente paso es explotar las distintas fuentes de alimento, lo cual se traduce en realizar modificaciones a la solución inicial obteniendo nuevas soluciones. En función de lo prometedores que sean los resultados, se dedicará mayor o menor tiempo a explotar la fuente de alimento tal y como se comportan las abejas realizando su danza en la colmena y provocando que otras abejas (las abejas observadoras) exploten también esa fuente de alimento. En el modelo propuesto por D. Karaboga, las nuevas soluciones se obtienen combinando las soluciones candidatas, utilizando la siguiente función:
v[i,g] = x[i,g] + Φ · (x[i,g] − x[k,g])
Donde v[i,g] representa la nueva solución obtenida, x[i,g] la solución en la que la abeja se encuentra en ese momento, x[k,g] una fuente de alimento (solución) diferente a la que se encuentra la abeja, Φ un número real aleatorio definido entre [-1,1] y «g» el número de ciclo por el que va el programa. Se puede observar que la nueva solución encontrada v[i,g] surge de combinar la solución inicial (x[i,g]) con el resto de soluciones de forma aleatoria (x[i,g]-x[k,g]).
- Tras un cierto número de ciclos (n_ciclos) sin mejorar la solución, se considera que la fuente de alimento se ha agotado, y se abandona guardando la mejor solución encontrada.
- Finalmete, las abejas empleadas en esa fuente de alimento, se convierten en abejas desempleadas, por lo que en el algoritmo, se buscarán nuevas soluciones y se intentarán explotar, repitiendose los puntos 1, 2 y 3 durante el número de iteraciones definidas (n_iter).
Como se puede observar por el tipo de combinación de las soluciones, este algoritmo no es diréctamente aplicable a la resolución del problema del cálculo de rutas, por lo que es necesario modificar el algoritmo para que proporcione buenas soluciones al aplicarlo al problema del cálculo de rutas.
Adaptación del algoritmo de colonia de abejas al cálculo de rutas utilizando programación paralela
Ya hace tiempo, que el aumento de velocidad del procesador de nuestro ordenador va ligado al número de núcleos que este posee, de forma que las tareas se puedan realizar de forma paralela en los distintos núcleos. La tendencia para aumentar la eficiencia de los nuevos algoritmos no es otra que aprovechar esa potencia de calculo que nos ofrece la programación paralela.
Existen diversas tecnologías para realizar programas que se ejecuten (de forma completa o parcial) de forma paralela, como puede ser el Parallel Studio de Intel, el CUDA en GPUs de Nvidia, etc. Me gustaría indicar, a pesar de que excede el objetivo de esta entrada, que la programación paralela multicore (propia del parallel studio de Intel) y la programación paralela multihilo (propia de las GPUs de Nvidia) son muy diferentes, y cada una puede ser más o menos interesante en función del problema ante el que nos encontremos.
Uno de los principales problemas que tiene esta tecnología es el compartir información entre los distintos procesos que se ejecutan en paralelo. En general, las técnicas metaheurísticas basadas en población (en particular lal técnica de colonia de abejas), intentan explorar distintos espacios de búsqueda de forma independiente, compartiendo muy poca información entre ellos, por lo que se pueden paralelizar siguiendo la siguiente estructura:
1. Se obtendrán tantas fuentes de alimento (soluciones iniciales) como procesos en paralelo se quieran ejecutar.
2. Durante un cierto número de ciclos (n_ciclos) se intentará mejorar cada una de las soluciones utilizando alguna de las técnicas que ya han sido explicadas en este artículo de forma independiente entre todos los procesos.
3. Tras ese número de iteraciones, se guardan las mejores soluciones obtenidas por cada proceso, se buscan nuevas soluciones y se repite el ciclo un número de veces definido por el usuario (n_iter).
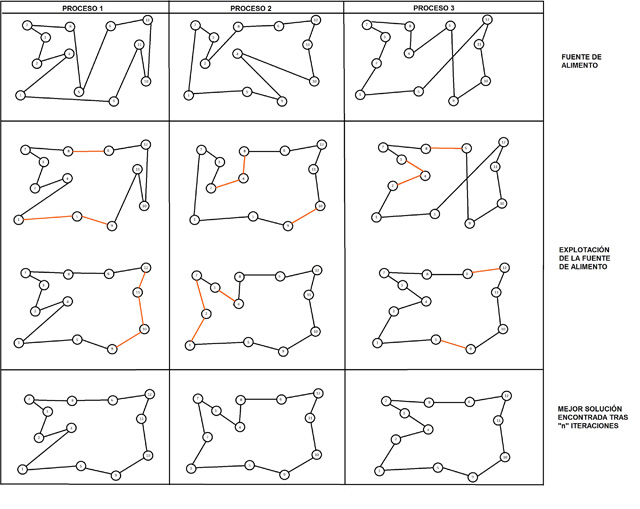
Se pueden probar diferentes versiones del algoritmo variando el número de soluciones que se modifican entre iteraciones:
- Cambiando todas las soluciones.
- Dejando las mejores soluciones y se modificando las demás (Elitist Bee System: EBS)
- Dejando las soluciones que han mejorado en los últimos k_ciclos y se modificando las demás (Promising Bee System: PBS).
Referencias
[1] D. Karaboga and B. Basturk. A powerful and efficient algorithm for numerical function optimization: Artificial bee colony (ABC) algorithm. Journal of Global Optimization, 39(3):459–471, 2007.
¿Quieres saber más sobre técnicas metaheurísticas? Contacta con nosotros sin compromiso.
Además, si quieres conocer mejor decide y mantenerte al tanto de futuras acciones, síguenos en las redes sociales (Linkedin, Twitter, Youtube).




